POKIPSY76
Simple no quiere decir fácil.
Y este problema, uno de los agujeros negros de las matemáticas, es prueba de ello.
El problema empieza dándote muchas posibilidades de cómo llamarlo:
Quizás el nombre más común sea la conjetura de Collatz, pues fue el matemático alemán Lothar Collatz quien primero la propuso en 1937.
Pero lo puedes encontrar como la conjetura de Ulam (por el matemático polaco-estadounidense Stanisław Marcin Ulam), el problema de Kakutani (por el matemático japonés-estadounidense Shizuo Kakutani), la conjetura de Thwaites(por el académico británico Sir Bryan Thwaites), el algoritmo de Hasse (por el matemático alemán Helmut Hasse) o el problema de Siracusa.
Y eso no es todo: a la secuencia de números involucrada se le conoce comosecuencia o números de granizo o como números maravillosos.
Quizás el nombre más descriptivo sea: la conjetura de 3n + 1.
Habiéndoselos presentado...
No es eso lo que enloquece a los matemáticos: llámese como se llame, sigue siendo el problema imposible más simple de todos.
Cualquier persona que sepa sumar, dividir y multiplicar puede entender de qué se trata, seguir la secuencia de números y hasta intentar resolverlo.
Pero, desde los años 30 del siglo pasado, nadie ha podido explicarlo, probarlo o refutarlo.
Nadie.
En algún momento se llegó a pensar que la conjetura era una estrategia soviética para distraer a los científicos.
Así que, antes de plantearles el problema, atendamos a una advertencia de uno de los matemáticos más prolíficos -y excéntricos- del siglo XX.
Las matemáticas no están listas para este tipo de problemas (...) Imposible, absolutamente imposible"
THINKSTOCK
Aquí está el problema:
Empiezas con un número entero natural cualquiera (1, 2, 3, 4, 5...).
- Si el número es par, lo divides por 2
- Si es impar, lo multiplicas por 3 y le sumas 1
Después, le aplicas esas mismas sencillas reglas al resultado.
Empecemos con 10, que es par.
10 ÷ 2 = 5, que es impar, así que aplicamos la segunda regla.
5 x 3 = 15 + 1 = 16.
Como es par... 16 ÷ 2 = 8
8 ÷ 2 = 4
4 ÷ 2 = 2
2 ÷ 2 = 1
Hasta aquí, sencillo.
Lo que desconcierta es que no importa con cuál número empieces, eventualmente siempre llegarás al 4 que se convierte en 2 y que termina en 1.
Al menos ese es el caso con todos los números que se ha probado, y se ha probado con algunos casi absurdos.
JASON DAVIES, INGENIERO Y VISUALIZADOR
Supercomputadoras lo han hecho con los que van hasta más o menos5.764.607.500.000.000.000.
Todos eventualmente llegan a 2 ÷ 2 = 1.
No obstante, como los números son infinitos, eso no prueba que ese sea el caso para todos los números naturales.
Pero como no se ha podido encontrar una excepción, tampoco hay prueba de que no sea así.
El otro interrogante sin resolver es el eterno por qué. ¿Por qué se comportan así los números?
Les debo advertir que no traten de resolverlo en la mente o calcularlo en el revés de un sobre viejo"
THINKSTOCK
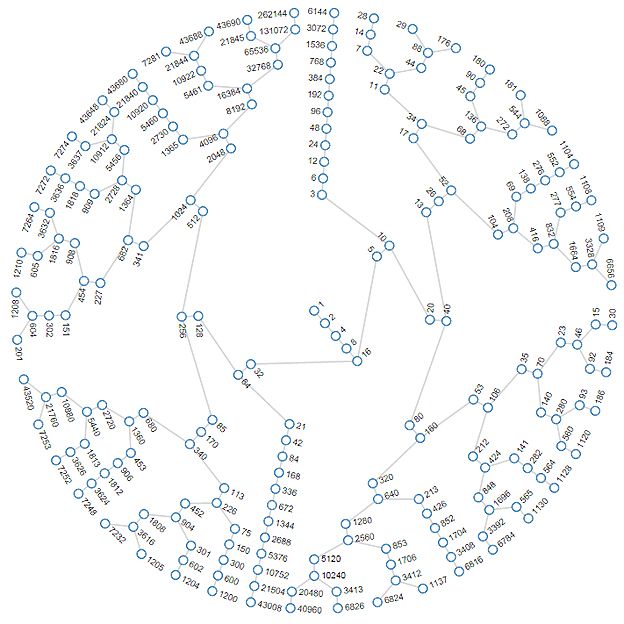
¿Recuerdas el granizo?
Dijimos que no importa cómo, el problema siempre se llega al mismo punto.
El lío es que a la hora de tratar de resolverlo diseñando un algoritmo, hay piedras de hielo en el camino.
Como el granizo en las nubes antes de caer, los números saltan de un lugar al otro antes de llegar al 4, 2, 1.
Unos más y unos menos, sin ton ni son.
KUNASHMILOVICH - CREATIVE COMMONS
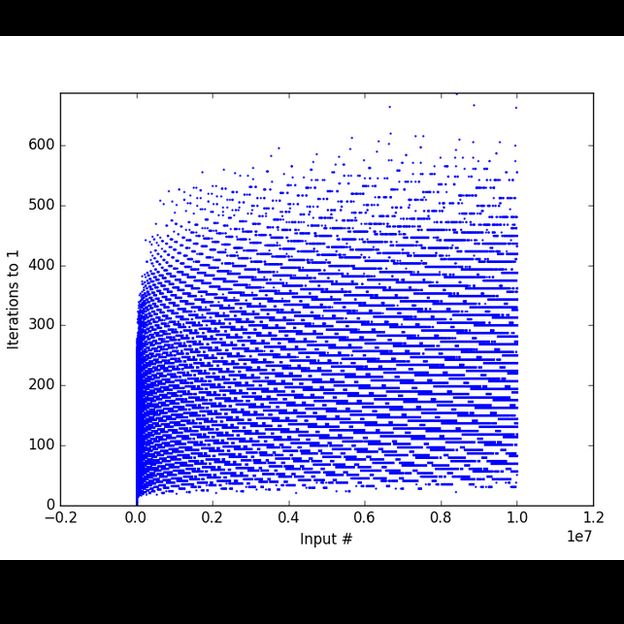
La mayor cantidad de escalas que hace un número inicial menor de 100 millones para llegar a 4, 2, 1 es 986.
Pero mientras que, por ejemplo, para los múltiplos de 2 el viaje es más corto, otros toman más tiempo.
Un ejemplo citado a menudo es la comparación entre los números 8.192 y 27.
Al 8.192 le toma 13 pasos llegar aparentemente ineludible final: 4, 2, 1.
El número 27 no sólo toma 111 pasos en llegar sino que en el camino sube hasta 9.232 antes de poder alcanzar al 8.192 en el 4, 2, 1.
La falta de patrones dificulta aún más resolver una conjetura ya tachada de imposible.
CARICATURA DE XKCD.COM/GABRIEL RODRÍGUEZ ALBERICHCurioso pero ¿importa?
Si es tan difícil, quizás imposible, resolverlo, ¿vale la pena seguir tratando?
"Cuando pases días o semanas tratando de resolver un problema en vano, piensa en el pobre Sísifo y su roca", aconsejó el geómetra Coxeter.
"Como (el matemático alemán) Felix Behrend dice al final de su libro, 'Sísifos y su roca son el símbolo del hombre y su eterna lucha, incesante, inalcanzable y, sin embargo, siempre triunfante. ¿Qué más se puede pedir?'".
Poético, pero si eso no te convence de la importancia de aclarar la incógnita, recurramos a los expertos de Mathematics Stack Exchange, el sitio de preguntas y respuestas para las personas que estudian matemáticas en cualquier nivel y profesionales de campos relacionados.
"Los matemáticos sospechan que solucionar la conjetura de Collatz abrirá nuevos horizontes y desarrollará nuevas e importantes técnicas en la teoría de los números", señaló Greg Muller.
"El problema de Collatz es lo suficientemente simple como para que cualquier persona lo entienda, y sin embargo, no sólo se relaciona con la teoría de números sino con problemas de decidibilidad, el caos y los fundamentos de las matemáticas y de computación. Mejor imposible", respondió Matt.
"Otra razón es que, por ser fácil de presentar y entender, tienen el potencial de atraer a los jóvenes a las matemáticas. Yo mismo me enteré de su existencia en la secundaria y no pude resistir su encanto", comentó Derek Jennings.
